Jesper E. van Engelen, A survey on semi-supervised learning
전통적인 supervised learning problem
- 학습 데이터는 $l$개의 라벨링된 data points의 ordered collection $D_L=((x_i, y_i))^l_{i=1}$다.
- 각각의 data point $(x_i, y_i)$는 주어진 input space $\chi$의 원소 $x_i \in \chi$와 그에 대응하는 label $y_i$로 이루어져 있다.
- $y_i$는 regression 문제에서는 실수 값이고, classification 문제에서는 카테고리 값이다.
- 이러한 data point는 training data라고 부른다.
- supervised learning은 이전에 본 적 없는 input $x^$에 대해서 라벨 $y^$를 결정하는 함수를 구한다.
Unlabelled data points
- 실제 classification 문제에서는 라벨을 알 수 없는 $u$ data points의 collection $D_U = (x_i)^{l+u}_{i=l+1}$를 알 수 있다.
- 예를 들어 보통 test data라 부르는 supervised learning에서 라벨을 예측해야 하는 data points가 있다.
- Semi-supervised classification은 이런 unlabelled data points를 이용해서 labelled data points만을 사용해서 학습을 했을 때보다 더 좋은 성능을 만들 수 있도록 학습한다.
- 이하에서 $X_L$과 $X_U$를 각각 labelled, unlabelled input object의 collection으로 나타낸다.
classification에서 unlabelled data의 이용
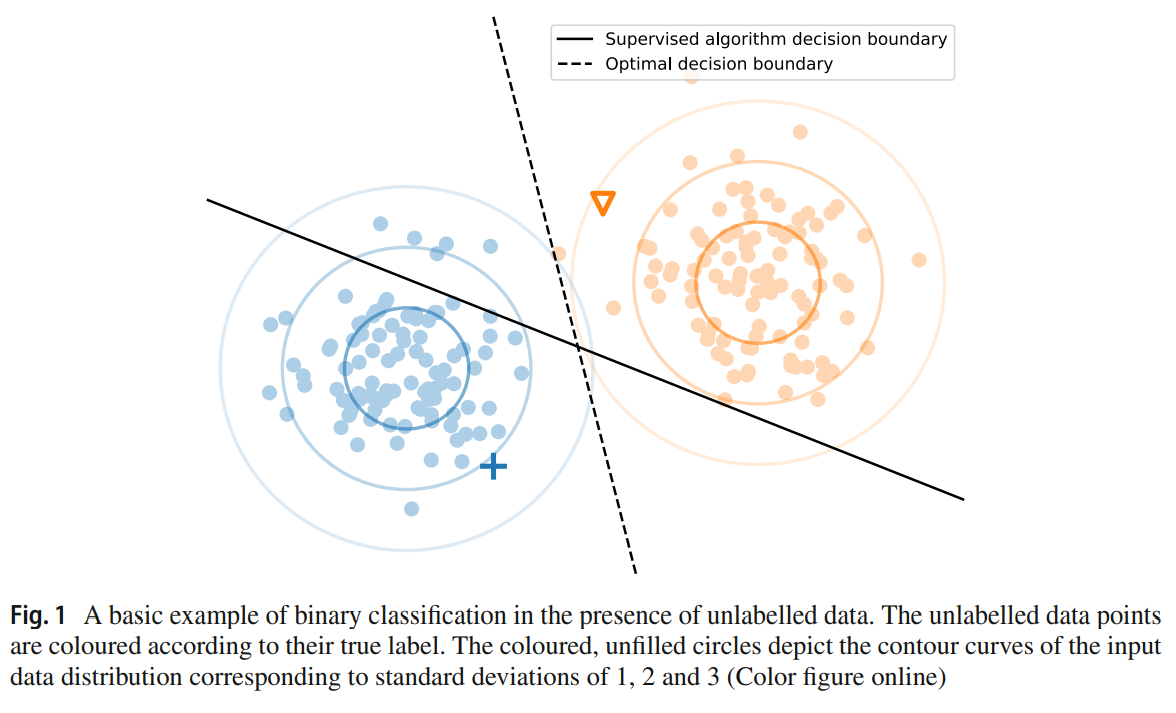
- Figure 1은 unlabelled data를 어떻게 사용할 것인지에 대한 이해를 돕는다.
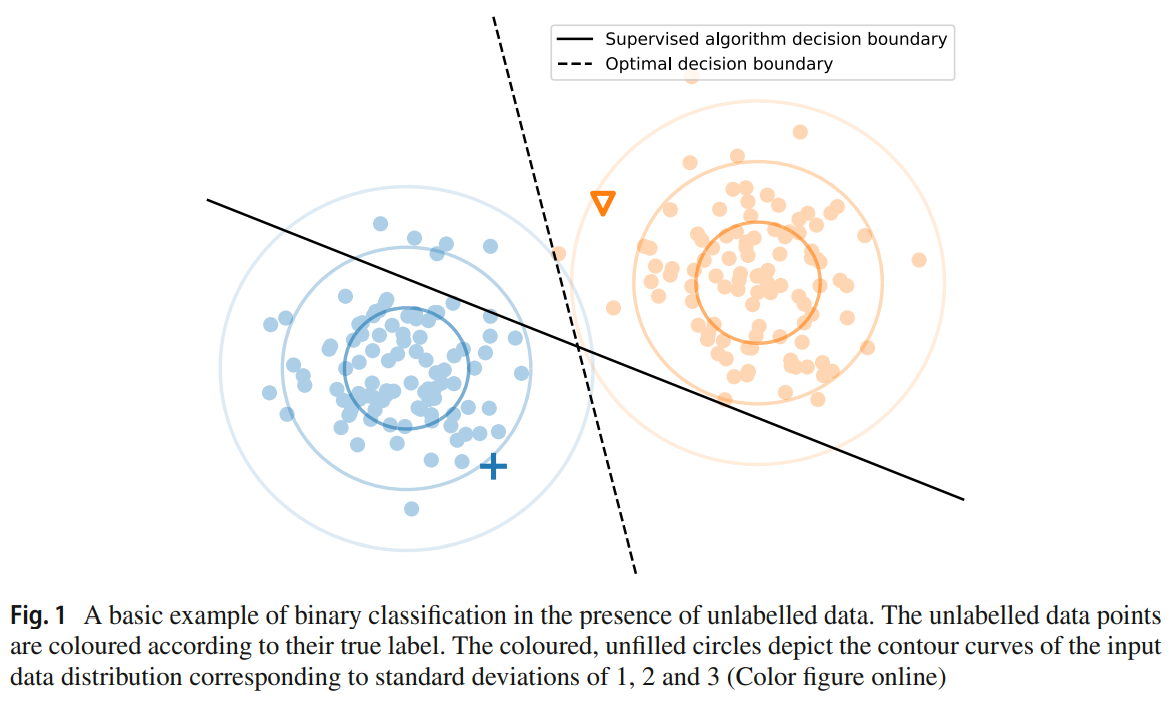
두 개의 class를 분류하는 문제가 있다.
- 두 class는 100개의 sample이 있으며, 이들은 각각 2차원에서 같은 covariance matrices로 Gaussian distribution을 따른다고 하자.
- Labelled data set은 각각의 class에서 하나의 sample로 구성되어 있다.
- Supervised learning 알고리즘은 두 점을 잇는 직선의 중점을 지나면서 수직인 경계를 class의 경계로 예측할 가능성이 높다. 그러나 이는 optimal decision boundary와는 거리가 있다.
- 그림에서 알 수 있듯이 unlabelled data의 cluster를 통해 class의 경계를 더 정확하게 예측할 수 있다.
“Semi-supervised learning의 가정”에서 계속