Sebastian Ruder, An overview of gradient descent optimization algorithms

Gradient descent

Gradient descent는 파라미터 $\theta \in \mathbb{R}^d$를 가지는 모델의 objective function $J(\theta)$을 최소화하는 알고리즘으로, objective function의 gradient $\nabla_\theta J(\theta)$의 반대 방향으로 파라미터를 업데이트 한다. Learning rate $\eta$는 최솟값에 도달하기 위해 얼마의 step으로 이동해야 하는지를 결정한다.

• we follow the direction of the slope of the surface created by the objective function downhill until we reach a valley

Batch gradient descent

가장 기본적인 vanilla gradient descent는 batch gradient descent이다. 모든 학습 데이터셋으로부터 $J(\theta)$의 gradient를 계산하여 $\theta$를 업데이트 한다.

\[\theta = \theta - \eta \nabla_\theta J(\theta)\]

한 번의 update를 위해 전체 데이터셋에서 gradient를 계산해야 하기 때문에 매우 느리고 메모리 문제가 있다. 또한, 새로운 데이터를 가지고 학습하지 못하는 단점이 있다.

하지만 convex한 error surface에서 글로벌 minimum에 도달하도록 보장하고, non-convex surface에서는 local minimum에 도달하도록 보장한다.

Stochastic gradient descent

Stochastic gradient descent(SGD)는 각 학습 샘플 $x^{(i)}$와 라벨 $y^{(i)}$마다 파라미터 업데이트를 진행한다.

\[\theta = \theta - \eta \nabla_\theta J(\theta;x^{(i)};y^{(i)})\]

Batch gradient descent는 큰 데이터셋에 대해서 반복해서 계산하기 때문에 비슷한 데이터에 대해서 항상 gradient를 다시 계산하여 파라미터를 업데이트한다. SGD의 경우는 반복을 업데이트할 때마다 수행한다. 따라서 SGD는 빠르면서 새로운 데이터에서도 학습을 할 수 있다. 더 잦은 파라미터의 업데이트로 objective function을 유동적으로 만들 수 있다.

Batch gradient descent가 파라미터의 상태에 따라서 최소로 수렴하게 할 수 있는데 반해서 SGD는 새로운 곳으로 이동해서 잠재적으로 더 좋은 local minima에 도달할 수 있다. 그러나 이는 글로벌 minimum에 수렴하기 어렵게 만들어 SGD가 overshooting되는 문제가 있다. 이런 문제를 해결하기 위해서 learning rate를 조금씩 감소한다면 SGD가 batch gradient descent와 비슷한 형태로 수렴하는 양상을 볼 수 있다.

Mini-batch gradient descent

Mini-batch gradient descent는 n개의 학습 데이터로 이루어진 mini-batch마다 파라미터를 업데이트 하는 방법이다.

\[\theta = \theta - \eta \nabla_\theta J(\theta ; x^{(i:i+n)};y^{(i:i+n)})\]

이 방법은 파라미터 업데이트의 변동성을 줄일 수 있어서 안정적인 수렴을 보장하면서 성능 측면 또한 보장할 수 있다. Mini-batch의 사이즈는 50에서 256 사이로 다양하다. 2의 거듭제곱으로 하는 것이 GPU 구조 상 빠르다는 말이 있다.

Challenges

Mini-batch gradient descent는 좋은 수렴을 보여주지만 몇 가지 문제가 있다.

• 적절한 learning rate를 정하는 것이 어렵다. 너무 작은 learning rate는 수렴이 느리고, 너무 큰 learning rate는 최소의 값으로 수렴하지 못하며 심지어 발산할 수도 있다.
• Learning rate schedule은 learning rate를 학습 중에 적절하게 조정해준다. 그러나 schedules 또한 데이터셋의 특성에 맞게 적절히 사용해야 한다.
• 추가로, 모든 파라미터의 업데이트에 동일한 learning rate가 적용되는 문제가 있다. 데이터가 sparse하고 feature들이 매우 다른 빈도를 갖고 있다면 드물게 등장하는 feature에 대해서 더 큰 learning rate를 적용하고 싶다.
• Neural network가 가지는 error function이 convex하지 않는 경우가 많다. 이 경우 local minimum으로 수렴하거나 안장점에서 진동할 수 있다.

Momentum

SGD는 하나의 차원이 다른 차원보다 더 가파른 영역에서 최소를 탐색하는데 어려움이 있다. 이 경우에는 SGD는 진동하면서 이동하는 양상을 보여 수렴이 느려진다.

Momentum은 SGD가 특정한 방향으로 이동하도록 도우면서 진동을 방지하는데 도움을 준다. $\gamma$만큼의 비율로 이전 스텝의 업데이트 벡터 $v_{t-1}$를 더해서 $v_t$를 구한다.

\[v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta)\] \[\theta = \theta - v_t\]

Momentum term $\gamma$는 일반적으로 0.9 근처의 값을 사용한다.

Momentum을 사용하는 것은 언덕 아래로 공을 굴리는 것과 같다. 공은 momentum를 받으면서 언덕을 내려가며 한 쪽 방향으로 점점 빨라진다. 이와 같은 현상은 파라미터 업데이트에서도 발생한다. Momuntum term은 같은 방향의 gradient로 가는 속도를 높여주고, 반대 방향의 gradient로 가는 속도를 줄인다. 그 결과 더 빠른 수렴을 얻을 수 있고, 진동하는 것을 막을 수 있다.

Nesterov accelerated gradient

Nesterov accelerated gradient(NAG)은 공이 언덕을 올라가려고 할 때, 이를 다시 늦추어 준다. Momentum에서 파라미터 $\theta$를 업데이트하기 위해 momentum term $\gamma v_{t-1}$을 계산하였다. 그러므로, $\theta - \gamma v_{t-1}$를 계산하는 것은 다음 위치에 대한 근사를 의미한다. NAG에서는 gradient를 현재의 위치 $\theta$에 대해서 계산하는 것이 아니라 다음 위치에서 계산한다.

\[v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta - \gamma v_{t-1})\] \[\theta = \theta- v_t\]

NAG에서도 momentum term $\gamma$는 0.9 근방으로 설정한다.

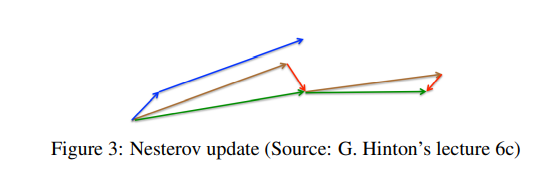
파란색 선은 momentum만 사용한 경우다. 이동 속도는 점점 빨라질 것이다. 갈색 선은 NAG에서 이전 이동을 나타내는 것이고, 빨간색 선 만큼 gradient가 반영되어 최종적으로 초록색 선만큼 이동한다. 속도의 증가는 크지 않다.

Adagrad

Adagrad는 드물게 업데이트 되는 파라미터에 데이서는 큰 업데이트를 하고, 자주 업데이트 되는 파라미터에 대해서는 작은 업데이트를 가져가도록 learning rate를 조정하는 방법이다. 그렇기 때문에 sparse한 데이터에 대해서도 좋은 최적화를 기대할 수 있다.

이전에는, 파라미터 $\theta$를 업데이트 할 때, 각각의 파라미터 $\theta_i$를 같은 learninga rate $\eta$를 적용해서 업데이트하였다. 모든 시점 t에 대해서 Adagrad는 파라미터 $\theta_i$에 대해서 다른 learning rate를 적용한다. $g_{t, i}$를 시점 $t$에서 파라미터 $\theta_i$에 대한 목적함수의 gradient라고 정의하자.

\[g_{t, i} = \nabla_{\theta_t}J(\theta_t, i)\]

SGD에서 시점 $t$에서 모든 파라미터 $\theta_i$의 업데이트는 아래와 같이 나타낼 수 있다.

\[\theta_{t+1, i} = \theta_{t, i} - \eta g_{t, i}\]

Adagrad는 시점 $t$에서 파라미터 $\theta_i$를 이전에 $\theta_i$에 대하여 계산되었던 gradient를 반영하여 learning rate $\eta$를 조정한다.

\[\theta_{t+1, i} = \theta_{t, i} - {\eta \over \sqrt{G_{t, ii} + \epsilon}}g_{t,i}\]

$G_t \in \mathbb{R}^{d \times d}$는 대각선의 원소 $i, i$가 시점 $t$까지 $\theta_i$가 업데이트 될 때 계산된 gradient의 제곱의 합인 대각행렬이다. $\epsilon$은 0으로 나누는 것을 방지하기 위한 term으로 보통 $1e-8$ 이하의 값을 사용한다. 위의 식을 element-wise matrix-vector multiplication $\odot$으로 나타내면

\[\theta_{t+1} = \theta_{t} - {\eta \over \sqrt{G_{t} + \epsilon}}\odot g_{t}\]

Adagrad의 장점은 일일히 learning rate를 튜닝할 필요가 없다는 점이다. learning rate는 대부분 0.01의 값을 사용한다. 반면 Adagrad의 단점은 gradient의 제곱이 점점 축적된다는 것이다. 더해지는 term이 모두 양수이면 점점 분모의 값은 커지게 되고 학습되는 정도는 점점 작아져 더 이상 학습이 진행되지 않게 되는 단점이 있다.

Adadelta

Adadelta는 Adagrad에서 learning rate가 너무 작아지는 겂을 방지한다. Adadelta는 이전의 gradient의 제곱이 축적되는 대신에 과거의 gradient를 고정된 사이즈 $w$로 제한한다.

Running average $E[g^2]_t$를 아래와 같이 재귀적으로 정의하자.

\[E[g^2] = \gamma E[g^2]_{t-1} + (1-\gamma)g_t^2\]

$\gamma$는 momentum term과 비슷하게 0.9 정도로 정의한다. SGD를 아래와 같이 다시 나타내자

\[\Delta \theta_t = - \eta g_{t,i}\] \[\theta_{t+1} = \theta + \Delta\theta_t\]

Adagrad에서 파라미터의 업데트는 vector는 아래와 같다.

\[\Delta \theta_t = -{\eta \over \sqrt{G_t + \epsilon}}\odot g_t\]

$G_t$를 $E[g^2]_t + \epsilon$으로 대체한다.

\[\Delta \theta_t = -{\eta \over \sqrt{E[g^2]_t + \epsilon}}\odot g_t\]

분모의 항은 gradient에 대한 root mean squared(RMS) error다.

\[\Delta \theta_t = -{\eta \over \sqrt{RMS[g]_t}}\odot g_t\]

또한, 파라미터에 대해서도 decaying average를 정의하였다.

\[E[\Delta \theta^2]_t = \gamma E[\Delta^2]_{t-1} + (1-\gamma)\Delta\theta_t^2\]

파라미터에 대한 root mean squared error는

\[RMS[\Delta\theta]_t = \sqrt{E[\Delta\theta^2]_t + \epsilon}\]

$RMS[\Delta\theta]_t$를 알지 못하기 때문에 이전 스텝의 파라미터의 RMS로 근사한다.

\[\theta_t = -{RMS[\Delta\theta]_{t-1}\over RMS[g]_t}g_t\] \[\theta_{t+1} = \theta_t + \Delta\theta_t\]

Adadelta의 경우 learning rate를 명시적으로 지정할 필요가 없다.

RMSprop

RMSprop는 unpublished된 adaptive learning rate method이다. Adadelta와 마찬가지로 Adagrad가 가진 learning rate가 매우 작아지는 문제를 해결하기 위해 만들어졌다. RMSprop는 Adadelta에서 유도했던 식과 유사하다.

\[E[g^2] = \gamma E[g^2]_{t-1} + (1-\gamma)g_t^2\] \[\theta_{t+1} = \theta_t-{\eta \over \sqrt{E[g^2]_t + \epsilon}}g_t\]

Adam

Adaptive Moment Estimation(Adam)은 RMSprop와 momentum을 모두 사용한 optimizer라 할 수 있다.

\[m_t = \beta_1m_{t-1} + (1 -\beta_1)g_t\] \[v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2\]

$m_t$와 $v_t$는 gradient의 first moment, second moment를 각각 의미한다.

\[\hat{m_t}={m_t\over{1-\beta_1^2}}\] \[\hat{v_t}={v_t\over{1-\beta_1^2}}\]

Adam의 업데이트는

\[\theta_{t+1} = \theta_t - {\eta \over \sqrt{ \hat{v_t} + \epsilon }} \hat{m_t}\]

Adam의 저자는 기본 값으로 $\beta_1$으로는 0.9, $\beta_2$로는 0.999, $\epsilon$으로는 $10^{-8}$을 제안하였다.

기타

Nadam, Adamax

Optimizer의 선택

만약 input data가 sparse하다면 adaptive learning-rate method를 채용한다. RMSprops는 Adagrad의 한계를 보정하였고, Adam은 RMSprops에 momentum을 도입해 더 좋은 성능을 보이는 것으로 알려졌다. 따라서, 일반적인 경우에는 Adam이 좋은 선택이다.